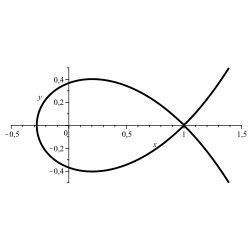Óvalo

Un óvalo cun eixo de simetría

O termo óvalo (do latín ovum, ovo) fai referencia a unha forma xeométrica convexa e redondeada, que se asemella ao perfil dun ovo de ave no seu sentido máis amplo. Inclúe as circunferencias e as elipses como casos especiais, con dous eixos de simetría en lugar de soamente un ou ningún. O uso do termo non sempre é consistente, en ocasións tamén se usa de maneira puramente descritiva. Con todo, na análise matemática pódese definir formalmente como un tipo de curvas planas. Neste contexto, tamén se fala de curvas ou liñas ovaladas. Un corpo convexo redondeado e tridimensional (xeralmente un subconxunto convexo pechado de $\mathbb {R} ^{n}$) coñécese como ovoide. Neste sentido, un óvalo cos puntos do seu interior é un ovoide de dúas dimensións.

En xeometría proxectiva os termos curva ovalada e ovoide (sen atender ás derivadas) segundo as súas condicións de convexidade, establécense utilizando exclusivamente condicións de incidencia ("cada recta curta un óvalo ou ovoide en como máximo dous puntos"), no que se define como un conxunto cuadrático. En sentido proxectivo, un óvalo no plano real require ademais a condición de que ningún punto do seu contorno teña curvatura nula. Tal óvalo é entón o bordo dun conxunto estritamente convexo, porque non contén segmentos rectilíneos.

Definición formal e propiedades

Óvalo sen eixos de simetría

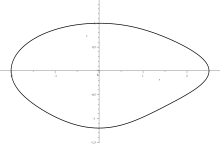
A forma redondeada dun óvalo é a consecuencia de que unha curva pechada reúna as condicións de suavidade e convexidade, de acordo coa seguinte definición:

Unha curva fechada plana, convexa e dúas veces continuamente diferenciable, denomínase óvalo

Porén, esta definición non abarca todas as figuras xeométricas que ás veces son denominadas óvalos. Por exemplo, os óvalos compostos por diferentes arcos circulares non cumpren esta definición, porque a súa segunda derivada non é continua en toda a curva. Se queremos contemplar tamén estes casos, entón debe prescindirse da condición da suavidade da curvatura (diferenciabilidade $C^{0}$ ou $C^{1}$ en lugar de $C^{2}$). En consecuencia, nalgúns textos a definición de óvalo só esixe a condición de convexidade. Con todo, isto ten a desvantaxe de que a definición inclúe entón figuras que apenas son percibidos con forma de ovo, tales como os polígonos convexos.

Óvalo con rectas tanxente, secante e pasante

• Un óvalo é unha curva de Jordan, é dicir, non ten bucles nin lazos.
• A orientación da curvatura dun óvalo non ten cambios de signo, é dicir, dependendo do sentido de percorrido. Isto significa que a curvatura orientada para cada punto do óvalo é sempre negativa ou sempre positiva. De maneira ilustrativa, isto significa que non presenta retrocesos nin fendas. Só pode percorrerse mediante un xiro completo de 360 ° á esquerda ou á dereita.
• O interior dun óvalo é un conxunto convexo, e o óvalo forma o seu bordo.
• Nun óvalo é aplicable o teorema dos catro vértices, é dicir, a súa lei de curvatura presenta polo menos catro puntos extremos.
• Se un punto do óvalo ten unha tanxente, todo o óvalo está ao mesmo lado da tanxente.
• Se ademais se esixe que a curvatura do óvalo non desapareza en ningunha sección, é dicir, que a curvatura adquira o valor cero como máximo en puntos illados, entón a tanxente anterior existe en cada punto do óvalo. Máis en xeral: entón, calquera liña recta ten en común co óvalo exactamente dous puntos (secante), un punto (tanxente) ou ningún punto (pasante).

Exemplos e construcións

Os óvalos pódense construír usando métodos completamente diferentes. Obtéñense varios procedementos de construción a partir de diversas técnicas de deseño da elipse conveniente modificadas. É sabido que se pode xerar unha elipse cortando un cono cun plano (véxase sección cónica). Se no canto dun cono se utiliza outro corpo de revolución como un hiperboloide, da intersección cun plano obtéñense diferentes óvalos. Unha posibilidade adicional consiste en substituír na ecuación paramétrica (ou na alxébrica) dunha elipse, os parámetros constantes a e b (as lonxitudes dos semieixos)

$(a\cdot \cos(t),b\cdot \sin(t))$

polas funcións

${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$

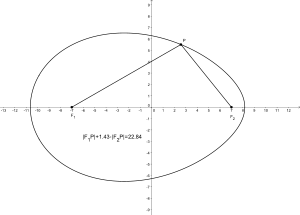
Tamén se pode definir unha elipse como o conxunto de puntos P, para os que a suma das distancias aos dous focos F₁ e F₂ é $\left(|F_{1}P|+|F_{2}P|=2a\right)$ constante.

Se se substitúe esta suma das distancias por unha suma ponderada $\left(k_{1}\cdot |F_{1}P|+k_{2}\cdot |F_{2}P|=2a\right)$, o conxunto de puntos forma un óvalo, que só ten un eixo de simetría, no que se sitúan un extremo romo e o outro puntiagudo. Tal óvalo coincide coa curva interior dun óvalo cartesiano.

O método de construción de Philippe de La Hire crea unha elipse usando dúas circunferencias concéntricas. Se desprazarmos un pouco o centro do círculo exterior e se conservan os pasos restantes do proceso de construción, obtense un (novo) óvalo, que posúe un eixo de simetría cando se move o centro do círculo exterior nos eixos da elipse. Se movemos o centro fóra dos eixos, créase un óvalo sen eixos de simetría.

• 
  Construción con circunferencias concéntricas
• 
  Construción con circunferencias excéntricas
• 
  Elipse:$|F_{1}P|+|F_{2}P|=22{,}84\,$
• 
  $|F_{1}P|+{\textbf {1.43}}\cdot |F_{2}P|=22{,}84$
• 
  Elipse:${\frac {x^{2}}{4}}+{\frac {y^{2}}{1}}=1$
• 
  ${\frac {x^{2}}{4}}+{\frac {y^{2}}{1-0{,}2\cdot x}}=1$

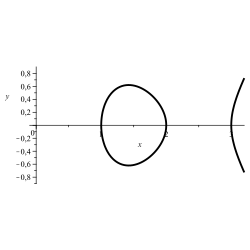
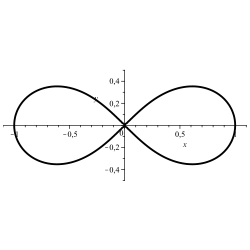
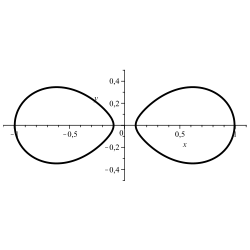
O conxunto de solucións dunha ecuación con dúas incógnitas ou certos dos seus subconxuntos a miúdo pódense considerar como curvas no plano. Unha ecuación adecuada produce un óvalo. Se tal curva solución do sistema non é ovalada, pero ten un bucle convexo, pódese crear un óvalo agregando un termo de corrección ao bucle.

• 
  Curva elíptica:$y^{2}=(x-1)\cdot (x-2)\cdot (x-3)$
• 
  Superelipse:$\left({\frac {x}{2}}\right)^{4}+\left({\frac {y}{1}}\right)^{4}=1$
• 
  Lemniscata:$(x^{2}+y^{2})^{2}-(x^{2}-y^{2})=0\,$
• 
  Óvalo de Cassini:$(x^{2}+y^{2})^{2}-(x^{2}-y^{2})+{\textbf {0,01}}=0$
• 
  Curva de Szegö:$x^{2}+y^{2}=e^{2\cdot x-2}$
• 
  $x^{2}+y^{2}+{\textbf {0,02}}=e^{2\cdot x-2}$
• 
  Folium de Descartes:$x^{3}+y^{3}=3\cdot x\cdot y$
• 
  $x^{3}+y^{3}+{\textbf {0,06}}=3\cdot x\cdot y$

Os óvalos tamén poden estar compostos por arcos e segmentos. Con todo, ditos óvalos teñen menos suavidade que a requirida na definición anterior, porque só verifican $C^{1}$ pero non $C^{2}$. Sendo aínda suaves no sentido dunha derivada constante, xa non teñen unha curvatura continua. A curvatura é constante nas seccións, pero presenta un punto de descontinuidade nas unións dos arcos circulares ou das seccións rectas.

Óvalos compostos de arcos circulares e seccións rectas

Exemplos de formas ovaladas comúns

• 
  Ilustración científica do século XIX
• 
  Ovos de galiña e de avestruz
• 
  Ovos de Pascua de Ucraína
• 
  Balón de rugby
• 
  Ovo de emú

Véxase tamén

Outros artigos

• Óvalo de Cassini
• Curva elíptica
• Superelipse

Bibliografía

• Ivanov, A.B. "Oval". 
• Helmut Reckziegel, Markus Kriener, Knut Pawel (1998). Elementare Differentialgeometrie mit Maple. Vieweg+Teubner Verlag. pp. 43 de 194. ISBN 9783528069919. Consultado o 28 de agosto de 2018. 
• Helmut Reckziegel, Markus Kriener, Knut Pawel (1998). Elementare Differentialgeometrie mit Maple. Vieweg+Teubner Verlag. pp. 43 de 194. ISBN 9783528069919. Consultado o 28 de agosto de 2018. 
• John A. Adam: A Mathematical Nature Walk. Princeton University Press 2009, ISBN 978-0-691-12895-5, S. 124–136
• Arnold Emch: Some Properties of Closed Convex Curves in a Plane. American Journal of Mathematics, Band 35, Nr. 4 (Okt., 1913), S. 407–41 Modelo:JSTOR*N. Hansen Ball: On Ovals. The American Mathematical Monthly, Band 37, Nr. 7 (Aug. - Sep., 1930), S. 348–353 Modelo:JSTOR
• Charles Hutton (1815). A Philosophical and Mathematical Dictionary. Volumen 2. author. p. 141. Consultado o 28 de agosto de 2018. 

Ligazóns externas

• Norbert Harthun, Iris Rennert: Die Ei-Kurve als Schnitt des Hyperbolischen KegelsArquivado 07 de setembro de 2012 en Wayback Machine. (PDF; 158 kB)
• Egg curves auf mathematische-basteleien.de (en inglés)
• Paul L. Rosin: On the Construction of Ovals Arquivado 25 de febreiro de 2021 en Wayback Machine. (PDF; 405 kB) (en inglés)
• André Heck: Mathematical Brooding over an Egg. In Loci, agosto de 2008 - Online-Journal der MAA
• Egg Math Arquivado 28 de abril de 2020 en Wayback Machine. - Sammlung von webbasierten Unterrichtseinheiten zur Mathematik rundum das Ei (en inglés)

• Bibliografía relacionada con Óvalo no catálogo da Biblioteca Nacional de Alemaña.