Número real: Diferenzas entre revisións
algo máis desde a wiki .es:Número real |
m arranxiño |
||
| Liña 2: | Liña 2: | ||
[[Ficheiro:Real number line.svg|miniatura|[[Número real|Recta real]].]] |
[[Ficheiro:Real number line.svg|miniatura|[[Número real|Recta real]].]] |
||
{{Números}} |
{{Números}} |
||
En [[matemáticas]], o conxunto dos '''números reais''' (denotado por <math>\mathbb{R}</math>) inclúe tanto aos [[número racional|números racionais]] (positivos, negativos e o [[cero]]) como aos [[número irracional|números irracionais]];<ref name=in>{{Cita libro |apelido=Arias Cabezas |apelido2=Maza Sáez |nome=José María |nome2=Ildefonso |ano=2008 |título=Matemáticas 1 |dataacceso=30 de abril de 2017 |páxina=13|capítulo=Aritmética y Álgebra |lugar=Madrid |editorial=Grupo Editorial Bruño, Sociedad Limitada |apelido-editor=Carmona Rodríguez |apelido-editor2=Díaz Fernández |nome-editor=Manuel |nome-editor2=Francisco Javier|isbn=9788421659854 |número-autores=2}}</ref> e noutro enfoque, [[número transcendente|transcendentes]] e [[número alxébrico|alxébricos]]. Os irracionais e os transcendentes<ref name="Tsipkin">''Manual de matemáticas'' (1985) Tsipkin, Editorial Mir, Moscú, |
En [[matemáticas]], o conxunto dos '''números reais''' (denotado por <math>\mathbb{R}</math>) inclúe tanto aos [[número racional|números racionais]] (positivos, negativos e o [[cero]]) como aos [[número irracional|números irracionais]];<ref name=in>{{Cita libro |apelido=Arias Cabezas |apelido2=Maza Sáez |nome=José María |nome2=Ildefonso |ano=2008 |título=Matemáticas 1 |dataacceso=30 de abril de 2017 |páxina=13|capítulo=Aritmética y Álgebra |lugar=Madrid |editorial=Grupo Editorial Bruño, Sociedad Limitada |apelido-editor=Carmona Rodríguez |apelido-editor2=Díaz Fernández |nome-editor=Manuel |nome-editor2=Francisco Javier|isbn=9788421659854 |número-autores=2}}</ref> e noutro enfoque, [[número transcendente|transcendentes]] e [[número alxébrico|alxébricos]]. Os irracionais e os transcendentes<ref name="Tsipkin">''Manual de matemáticas'' (1985) Tsipkin, Editorial Mir, Moscú, tradución de Shapovalova; pg. 86</ref> (1970) non se poden expresar mediante unha [[Fracción (matemáticas)|fracción]] de dous enteiros con denominador non nulo; teñen infinitas cifras decimais aperiódicas, tales como: √<span style="border-top:1px solid #000">5</span>, {{math|π}}, o número real {{math|log}}2, cuxa transcendencia foi enunciada por [[Leonhard Euler|Euler]] no século XVIII.<ref name="Tsipkin"/> |
||
Os números reais poden ser descritos e construídos de varias formas, algunhas simples aínda que carentes do rigor necesario para os propósitos formais de matemáticas e outras máis complexas pero co rigor necesario para o traballo matemático formal. |
Os números reais poden ser descritos e construídos de varias formas, algunhas simples aínda que carentes do rigor necesario para os propósitos formais de matemáticas e outras máis complexas pero co rigor necesario para o traballo matemático formal. |
||
Revisión como estaba o 28 de novembro de 2018 ás 11:50
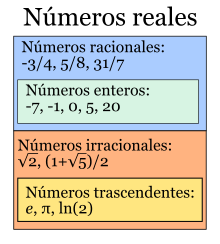

| Sistema numérico en matemáticas |
|---|
|
Conxuntos numéricos ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ |
| Números destacables |
| Outras extensións dos números complexos |
| Infinito |
| Especiais |
| Outros importantes |
| Sistemas de numeración |
En matemáticas, o conxunto dos números reais (denotado por ) inclúe tanto aos números racionais (positivos, negativos e o cero) como aos números irracionais;[1] e noutro enfoque, transcendentes e alxébricos. Os irracionais e os transcendentes[2] (1970) non se poden expresar mediante unha fracción de dous enteiros con denominador non nulo; teñen infinitas cifras decimais aperiódicas, tales como: √5, π, o número real log2, cuxa transcendencia foi enunciada por Euler no século XVIII.[2]
Os números reais poden ser descritos e construídos de varias formas, algunhas simples aínda que carentes do rigor necesario para os propósitos formais de matemáticas e outras máis complexas pero co rigor necesario para o traballo matemático formal.
Durante os séculos XVI e XVII o cálculo avanzou moito aínda que carecía dunha base rigorosa, debido a que no momento prescindían do rigor e fundamento lóxico, tan esixente nos enfoques teóricos da actualidade, e usábanse expresións como «pequeno», «límite», «achégase» sen unha definición precisa. Isto levou a unha serie de paradoxos e problemas lóxicos que fixeron evidente a necesidade de crear unha base rigorosa para a matemática, a cal consistiu de definicións formais e rigorosas (aínda que certamente técnicas) do concepto de número real.[3] Nunha sección posterior describiranse dúas das definicións precisas máis usuais actualmente: clases de equivalencia de sucesións de Cauchy de números racionais e cortaduras de Dedekind.
Notas
- ↑ Arias Cabezas, José María; Maza Sáez, Ildefonso (2008). "Aritmética y Álgebra". En Carmona Rodríguez, Manuel; Díaz Fernández, Francisco Javier. Matemáticas 1. Madrid: Grupo Editorial Bruño, Sociedad Limitada. p. 13. ISBN 9788421659854.
- ↑ 2,0 2,1 Manual de matemáticas (1985) Tsipkin, Editorial Mir, Moscú, tradución de Shapovalova; pg. 86
- ↑ Anglin, W. S. (1991). Mathematics: A concise history and philosophy. Springer. ISBN 3-540-94280-7.
Véxase tamén
| Wikimedia Commons ten máis contidos multimedia na categoría: Número real |
Outros artigos
Este artigo sobre matemáticas é, polo de agora, só un bosquexo. Traballa nel para axudar a contribuír a que a Galipedia mellore e medre.
Existen igualmente outros artigos relacionados con este tema nos que tamén podes contribuír. |















